マンデルブロ集合

Wed Aug 16 07:48:20 JST 2000
マンデルブロ集合を描いてみたいとしばらく思っていました。
あまり凝ったものではないけれどともかく第１号ができて念願がかなったというかんじです。でもgifの圧縮も荒っぽくていまいち。

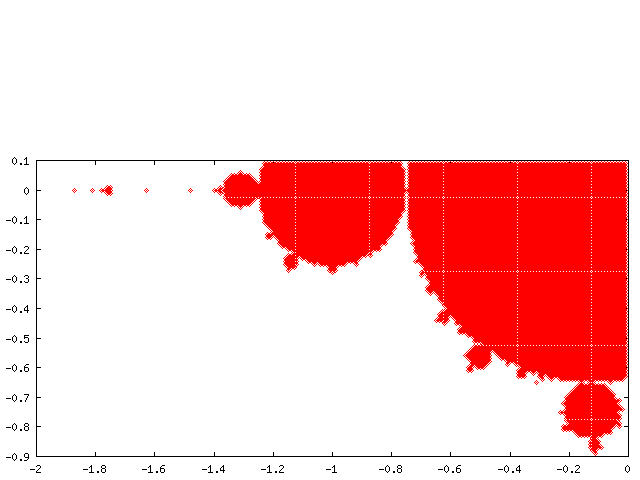
作成記
以前にもマンデルブロ集合を描こうとしたときがありました。
そのときは

	C(k) = C(k-1)*C(k-1) + C(0)
	C(i)は複素数

の軌跡をいろいろかいてみたのだと思います。
この結果はぐるぐるうずまきが描けるだけで、美しいフラクタル模様などさっぱりでてきません。

実はこの式はマンデルブロ集合自体ではなく、ある点がマンデルブロ集合の要素かどうか判定するための条件の一部だったのです。
C(k)が発散しないときC(0)はマンデルブロ集合に含まれます。
マンデルブロ集合を描こうと思ったら、ある空間の１点１点について、その座標をC(0)に代入します。C(k)が無限遠に飛んで行くかどうか確かめ、飛んで行かないならプロットして、飛んで行ってしまうならプロットしません。このようにしてプロットしたグラフがマンデルブロ集合になります。

判定に関して
実際の判定にあたって、どれだけ遠くに行けば発散したことにするのかは問題になるところです。しかし、原点からの距離が2以上になると発散することが証明されているそうです。今回はこれを信じました。もしかすると簡単に証明できるのかもしれないけど、そこまでやる元気はないです。
あと、C(k)を何回飛ばすかも迷うところです。今回は500回飛ばして距離が2以上にならなければマンデルブロ集合の要素であると判定しました。つまり、C(500)の点の原点からの距離が2未満ならその先で発散するかもしれないけど、とりあえず収束するものだと考えた、ということです。

プログラムについて
グラフの描画は他のソフトにまかせることにして、マンデルブロ集合の座標だけテキストで書き出すことにしました。グラフィックに関する知識があればもっと凝ったこともできそうな気もしますが、ともかく描いてみようということです。
言語について
はじめはperlで書いていましたが、あとからCに書き直しました。
日常的にはほとんどperlでスクリプトを書いているのでperlでかきはじめたのですが、今回の計算に関しては多少遅さを感じたので、perlで書いたものをCに書き直して実行しました。
コンパイルはgccでしましたが、math.hを使っているので -lm オプションをつけてコンパイルしてください。この事をしらなかったのでsqrtなどの数学関数を何度もはじかれてしまいました。京都産業大学の電算室のホームページでこのオプションを見つけて、なんとか成功しました。
perlのソース
Cのソース

画像について
数値のプロットは gnuplot を使いました。gifで出力しています。データの形式は、数値はx座標、y座標は空白で区切り、各点は改行で区切っています。Excelやほかのものでもグラフは描けるので、好きなものを使ってください。

参考書
カオスとフラクタル◎Excelで体験
臼田昭司他著
オーム社

この本はExcelでもマンデルブロ集合を描けるという趣旨の本なのですが、とてもわかりやすく説明してあります。この本がなければたぶん今回のプログラムは作れなかったでしょう。1年前ぐらいはExcelをこよなく愛してやまなかったのに、いまではまったく使ってないですね。強力なUNIXのツールたちにExcelが完敗したということでしょうか。

カオスの素顔
二ーナホール著
ブルーバックスB-1029

カオスについての概説書。
C(k) = C(k-1)*C(k-1) + C(0)
の式をはじめて見た本。この本を買ったときは結局C(k)の軌跡のうずまきを描いただけだった。よく読んでなくて理解が浅いせいもあったろうけど、この本だけでマンデルブロ集合を描くのはむりだったんだと思います。
ちょっと難しいきもするけどカオスの解説書としてはおもしろいとおもいます。